Calculates the DPIT residuals for regression models with discrete outcomes.
Specifically, the model assumption of GLMs with binary, ordinal, Poisson,
and negative binomial outcomes
can be assessed using resid_disc().
Usage
resid_disc(model, plot=TRUE, scale="normal", line_args=list(), ...)Arguments
- model
Model object (e.g.,
glm,glm.nb,polr)- plot
A logical value indicating whether or not to return QQ-plot
- scale
You can choose the scale of the residuals among
normalanduniformscales. The sample quantiles of the residuals are plotted against the theoretical quantiles of a standard normal distribution under the normal scale, and against the theoretical quantiles of a uniform (0,1) distribution under the uniform scale. The default scale isnormal.- line_args
A named list of graphical parameters passed to
graphics::abline()to modify the reference (red) 45° line in the QQ plot. If left empty, a default red dashed line is drawn.- ...
Additional graphical arguments passed to
stats::qqplot()for customizing the QQ plot (e.g.,pch,col,cex,xlab,ylab).
Details
The DPIT residual for the \(i\)th observation is defined as follows:
$$\hat{r}(Y_i|X_i) = \hat{G}\bigg(\hat{F}(Y_i|\mathbf{X}_i)\bigg)$$
where
$$\hat{G}(s) = \frac{1}{n-1}\sum_{j=1, j \neq i}^{n}\hat{F}\bigg(\hat{F}^{(-1)}(\mathbf{X}_j)\bigg|\mathbf{X}_j\bigg)$$
and \(\hat{F}\) refers to the fitted cumulative distribution function.
When scale="uniform", DPIT residuals should closely follow a uniform distribution, otherwise it implies model deficiency.
When scale="normal", it applies the normal quantile transformation to the DPIT residuals
$$\Phi^{-1}\left[\hat{r}(Y_i|\mathbf{X}_i)\right],i=1,\ldots,n.$$ The null pattern is the standard normal distribution in this case.
Check reference for more details.
References
Yang, Lu. "Double Probability Integral Transform Residuals for Regression Models with Discrete Outcomes." arXiv preprint arXiv:2308.15596 (2023).
Examples
library(MASS)
n <- 500
set.seed(1234)
## Negative Binomial example
# Covariates
x1 <- rnorm(n)
x2 <- rbinom(n, 1, 0.7)
### Parameters
beta0 <- -2
beta1 <- 2
beta2 <- 1
size1 <- 2
lambda1 <- exp(beta0 + beta1 * x1 + beta2 * x2)
# generate outcomes
y <- rnbinom(n, mu = lambda1, size = size1)
# True model
model1 <- glm.nb(y ~ x1 + x2)
resid.nb1 <- resid_disc(model1, plot = TRUE, scale = "uniform")
 # Overdispersion
model2 <- glm(y ~ x1 + x2, family = poisson(link = "log"))
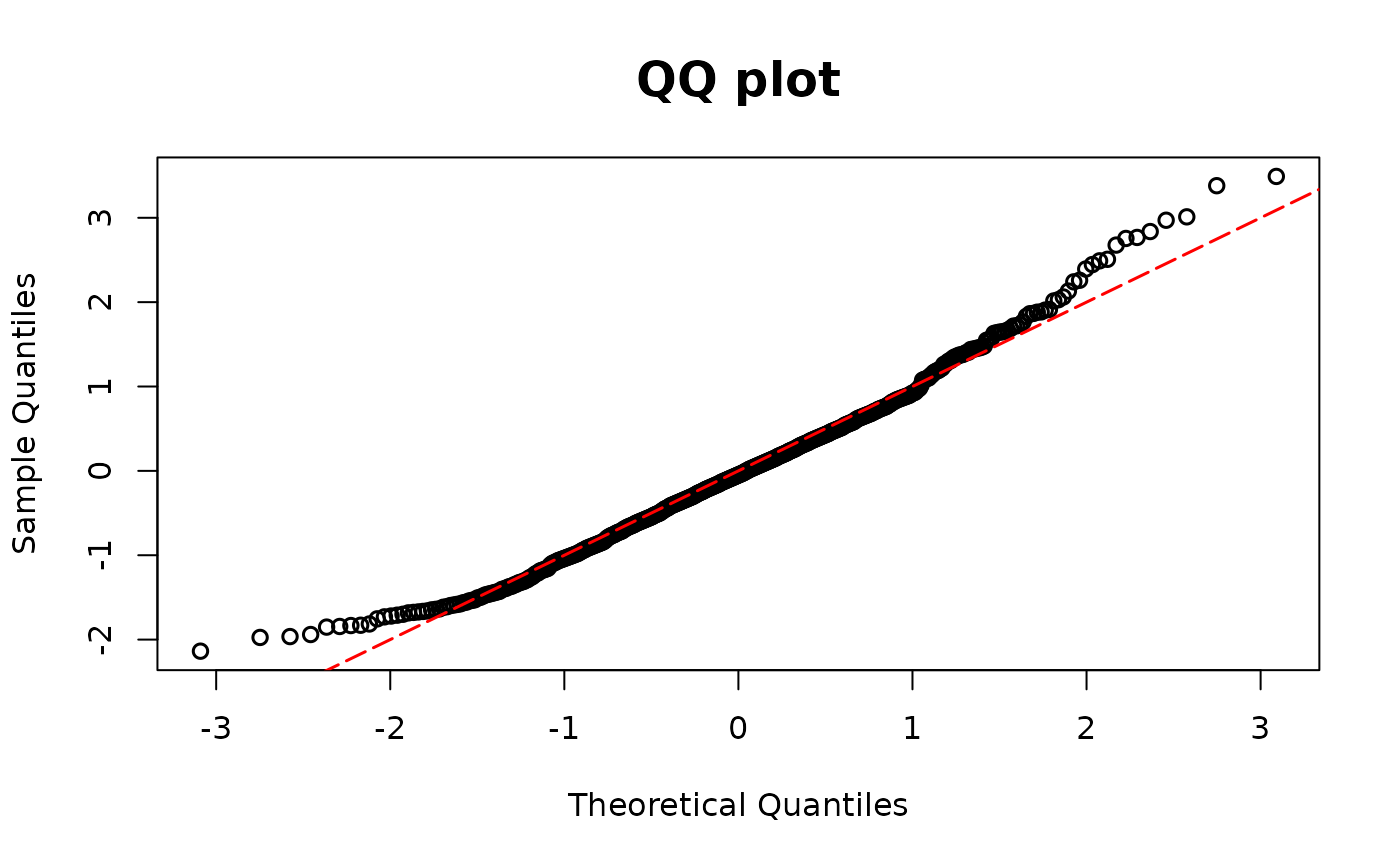
resid.nb2 <- resid_disc(model2, plot = TRUE, scale = "normal")
# Overdispersion
model2 <- glm(y ~ x1 + x2, family = poisson(link = "log"))
resid.nb2 <- resid_disc(model2, plot = TRUE, scale = "normal")
 ## Binary example
n <- 500
set.seed(1234)
# Covariates
x1 <- rnorm(n, 1, 1)
x2 <- rbinom(n, 1, 0.7)
# Coefficients
beta0 <- -5
beta1 <- 2
beta2 <- 1
beta3 <- 3
q1 <- 1 / (1 + exp(beta0 + beta1 * x1 + beta2 * x2 + beta3 * x1 * x2))
y1 <- rbinom(n, size = 1, prob = 1 - q1)
# True model
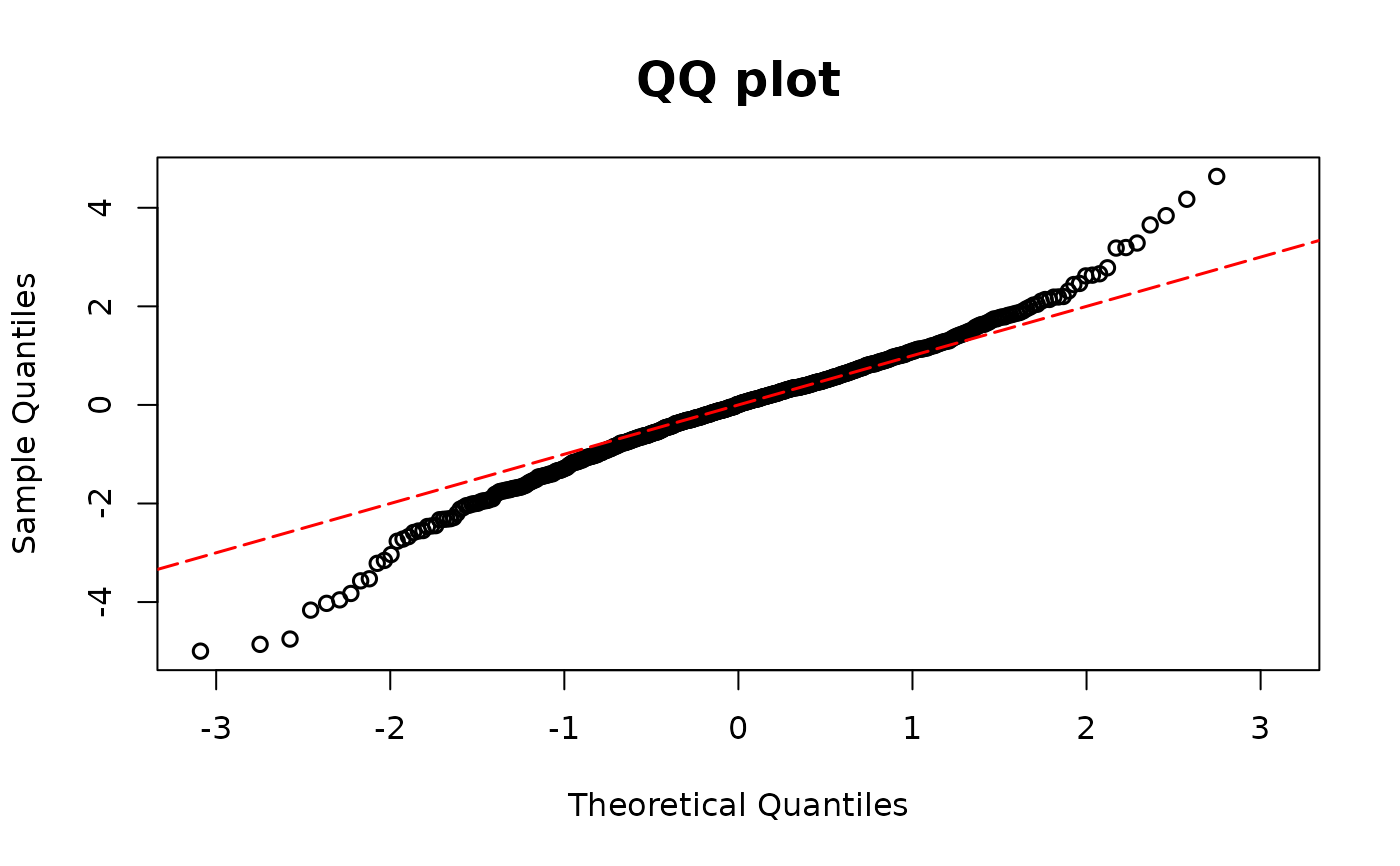
model01 <- glm(y1 ~ x1 * x2, family = binomial(link = "logit"))
resid.bin1 <- resid_disc(model01, plot = TRUE)
## Binary example
n <- 500
set.seed(1234)
# Covariates
x1 <- rnorm(n, 1, 1)
x2 <- rbinom(n, 1, 0.7)
# Coefficients
beta0 <- -5
beta1 <- 2
beta2 <- 1
beta3 <- 3
q1 <- 1 / (1 + exp(beta0 + beta1 * x1 + beta2 * x2 + beta3 * x1 * x2))
y1 <- rbinom(n, size = 1, prob = 1 - q1)
# True model
model01 <- glm(y1 ~ x1 * x2, family = binomial(link = "logit"))
resid.bin1 <- resid_disc(model01, plot = TRUE)
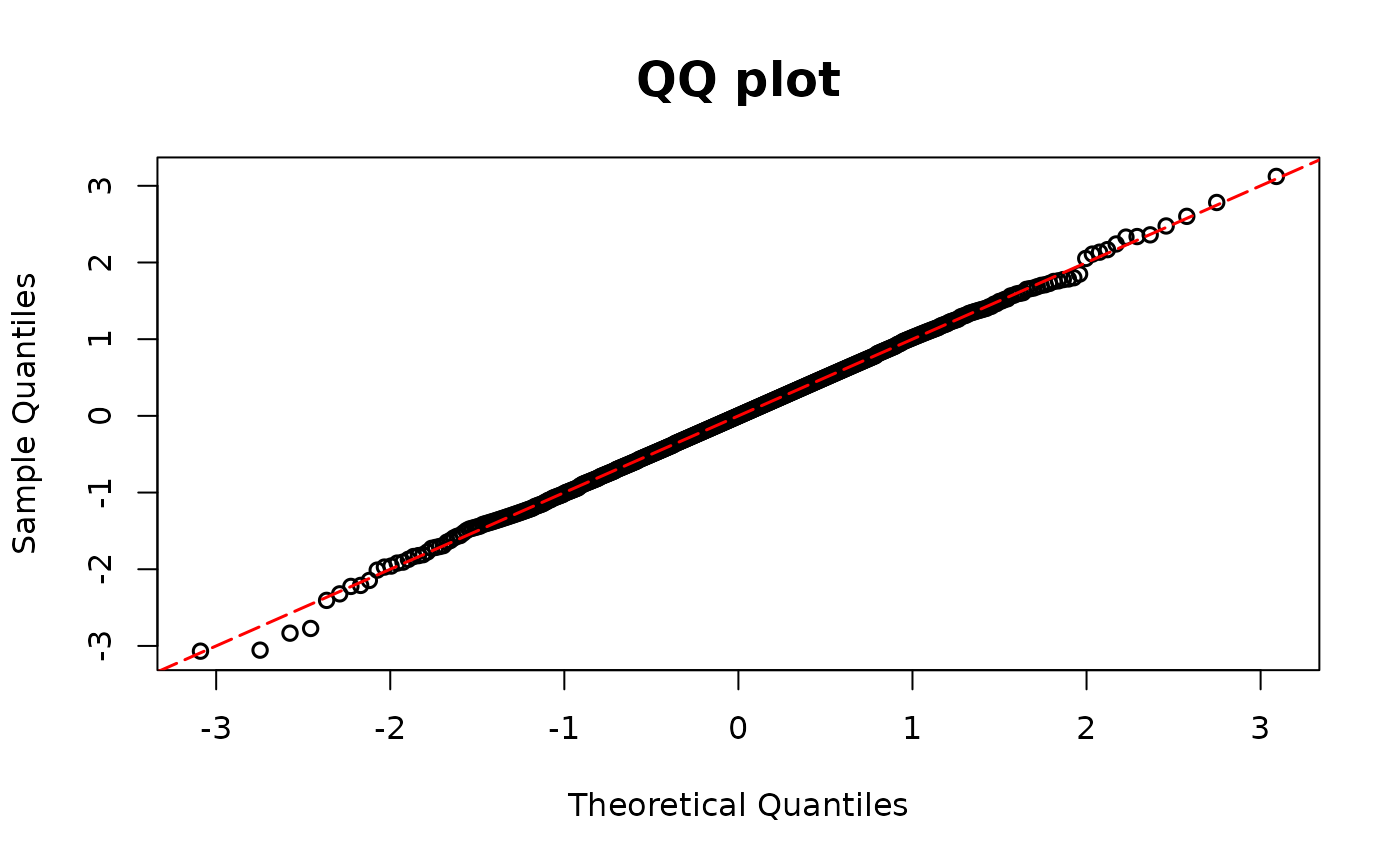 # Missing covariates
model02 <- glm(y1 ~ x1, family = binomial(link = "logit"))
resid.bin2 <- resid_disc(model02, plot = TRUE)
# Missing covariates
model02 <- glm(y1 ~ x1, family = binomial(link = "logit"))
resid.bin2 <- resid_disc(model02, plot = TRUE)
 ## Poisson example
n <- 500
set.seed(1234)
# Covariates
x1 <- rnorm(n)
x2 <- rbinom(n, 1, 0.7)
# Coefficients
beta0 <- -2
beta1 <- 2
beta2 <- 1
lambda1 <- exp(beta0 + beta1 * x1 + beta2 * x2)
y <- rpois(n, lambda1)
# True model
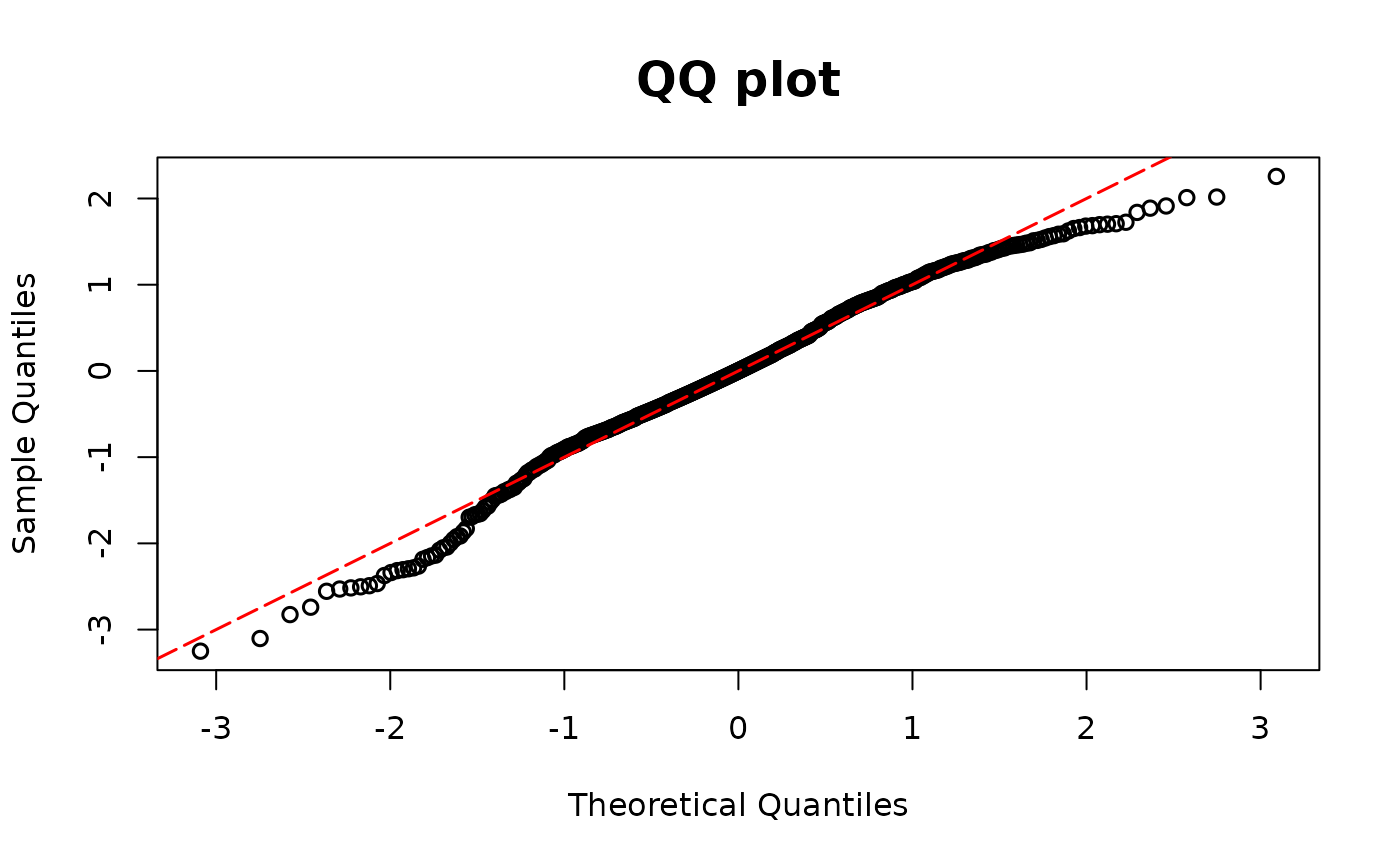
poismodel1 <- glm(y ~ x1 + x2, family = poisson(link = "log"))
resid.poi1 <- resid_disc(poismodel1, plot = TRUE)
## Poisson example
n <- 500
set.seed(1234)
# Covariates
x1 <- rnorm(n)
x2 <- rbinom(n, 1, 0.7)
# Coefficients
beta0 <- -2
beta1 <- 2
beta2 <- 1
lambda1 <- exp(beta0 + beta1 * x1 + beta2 * x2)
y <- rpois(n, lambda1)
# True model
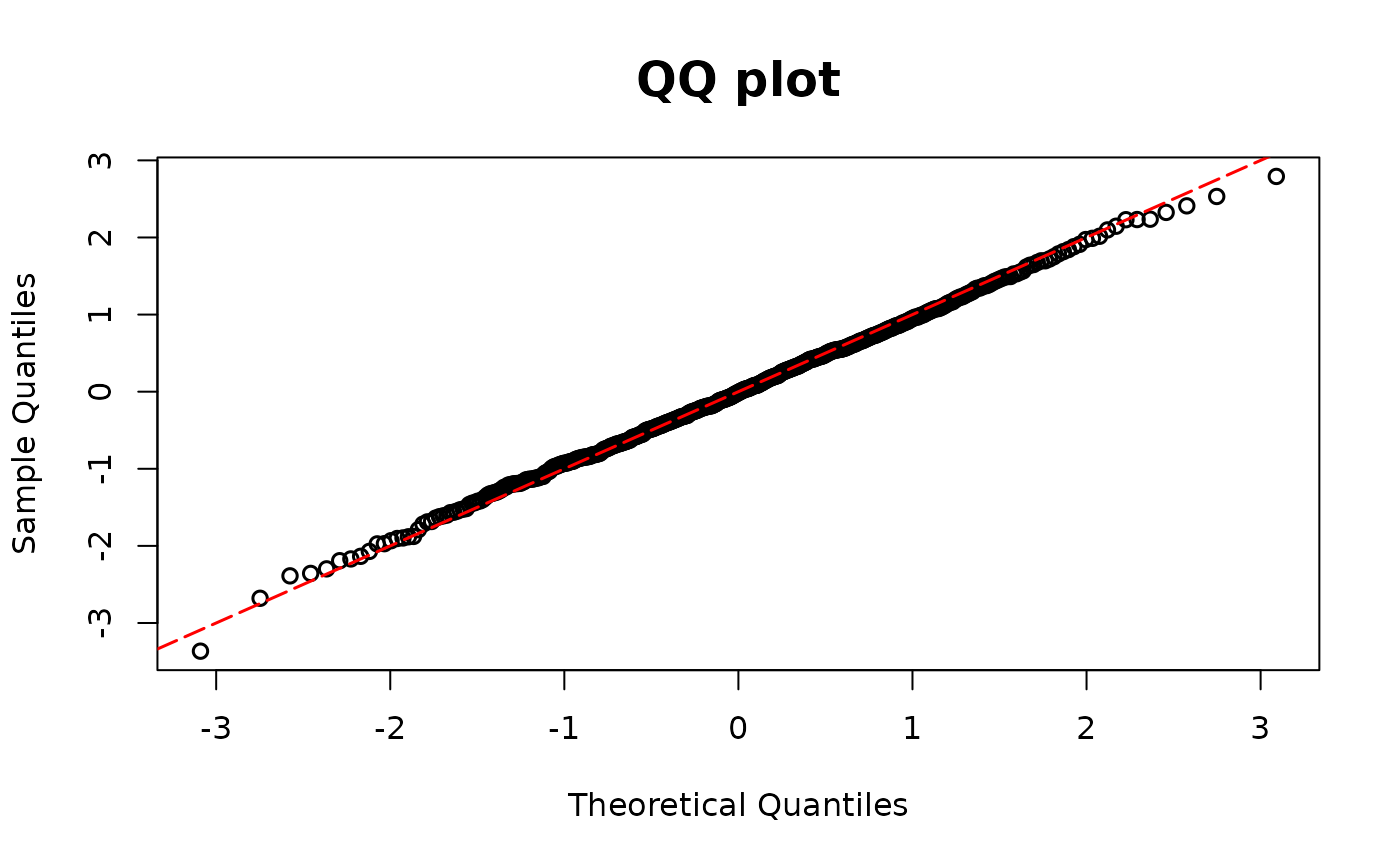
poismodel1 <- glm(y ~ x1 + x2, family = poisson(link = "log"))
resid.poi1 <- resid_disc(poismodel1, plot = TRUE)
 # Enlarge three outcomes
y <- rpois(n, lambda1) + c(rep(0, (n - 3)), c(10, 15, 20))
poismodel2 <- glm(y ~ x1 + x2, family = poisson(link = "log"))
resid.poi2 <- resid_disc(poismodel2, plot = TRUE)
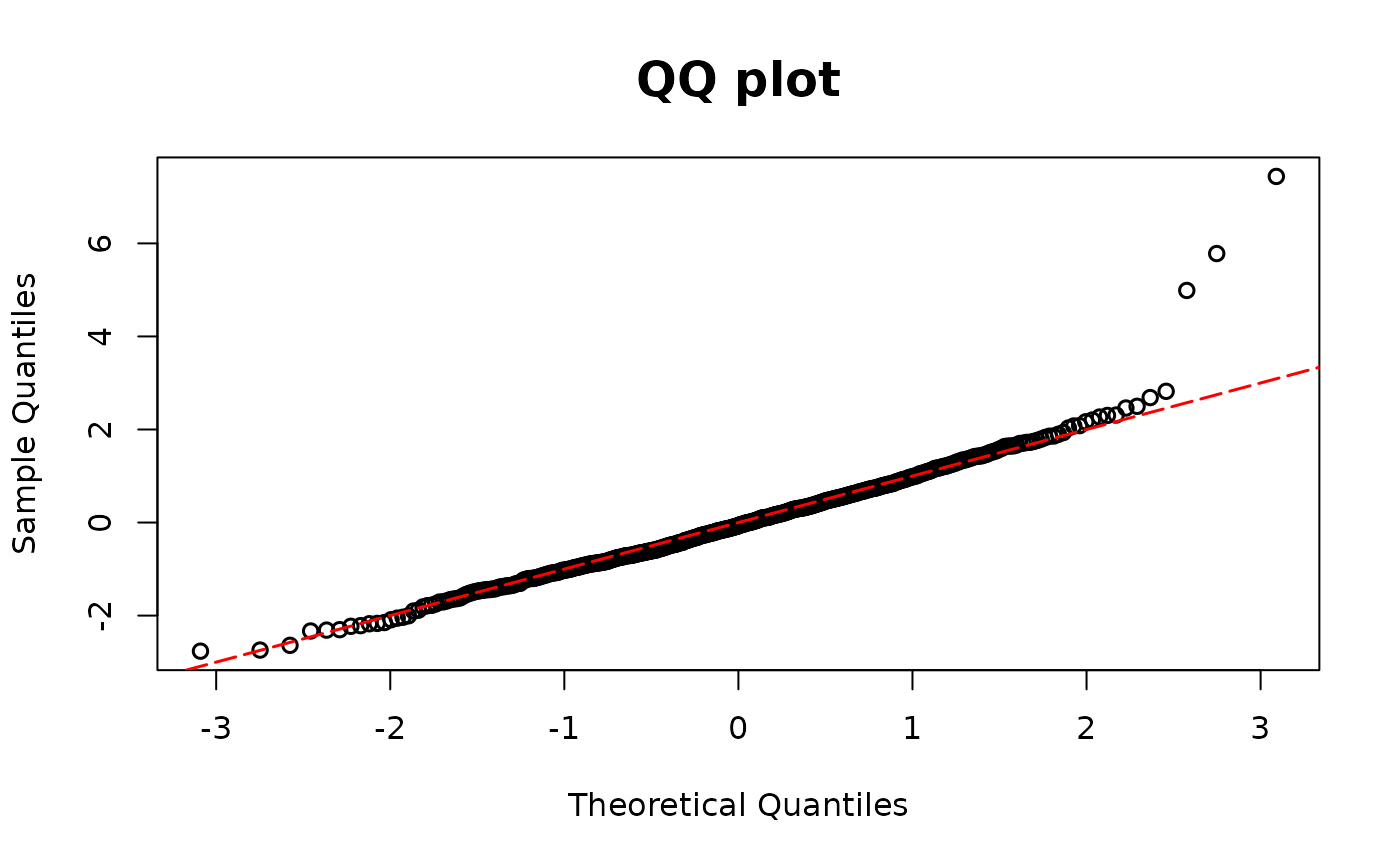
# Enlarge three outcomes
y <- rpois(n, lambda1) + c(rep(0, (n - 3)), c(10, 15, 20))
poismodel2 <- glm(y ~ x1 + x2, family = poisson(link = "log"))
resid.poi2 <- resid_disc(poismodel2, plot = TRUE)
 ## Ordinal example
n <- 500
set.seed(1234)
# Covariates
x1 <- rnorm(n, mean = 2)
# Coefficient
beta1 <- 3
# True model
p0 <- plogis(1, location = beta1 * x1)
p1 <- plogis(4, location = beta1 * x1) - p0
p2 <- 1 - p0 - p1
genemult <- function(p) {
rmultinom(1, size = 1, prob = c(p[1], p[2], p[3]))
}
test <- apply(cbind(p0, p1, p2), 1, genemult)
y1 <- rep(0, n)
y1[which(test[1, ] == 1)] <- 0
y1[which(test[2, ] == 1)] <- 1
y1[which(test[3, ] == 1)] <- 2
multimodel <- polr(as.factor(y1) ~ x1, method = "logistic")
resid.ord1 <- resid_disc(multimodel, plot = TRUE)
## Ordinal example
n <- 500
set.seed(1234)
# Covariates
x1 <- rnorm(n, mean = 2)
# Coefficient
beta1 <- 3
# True model
p0 <- plogis(1, location = beta1 * x1)
p1 <- plogis(4, location = beta1 * x1) - p0
p2 <- 1 - p0 - p1
genemult <- function(p) {
rmultinom(1, size = 1, prob = c(p[1], p[2], p[3]))
}
test <- apply(cbind(p0, p1, p2), 1, genemult)
y1 <- rep(0, n)
y1[which(test[1, ] == 1)] <- 0
y1[which(test[2, ] == 1)] <- 1
y1[which(test[3, ] == 1)] <- 2
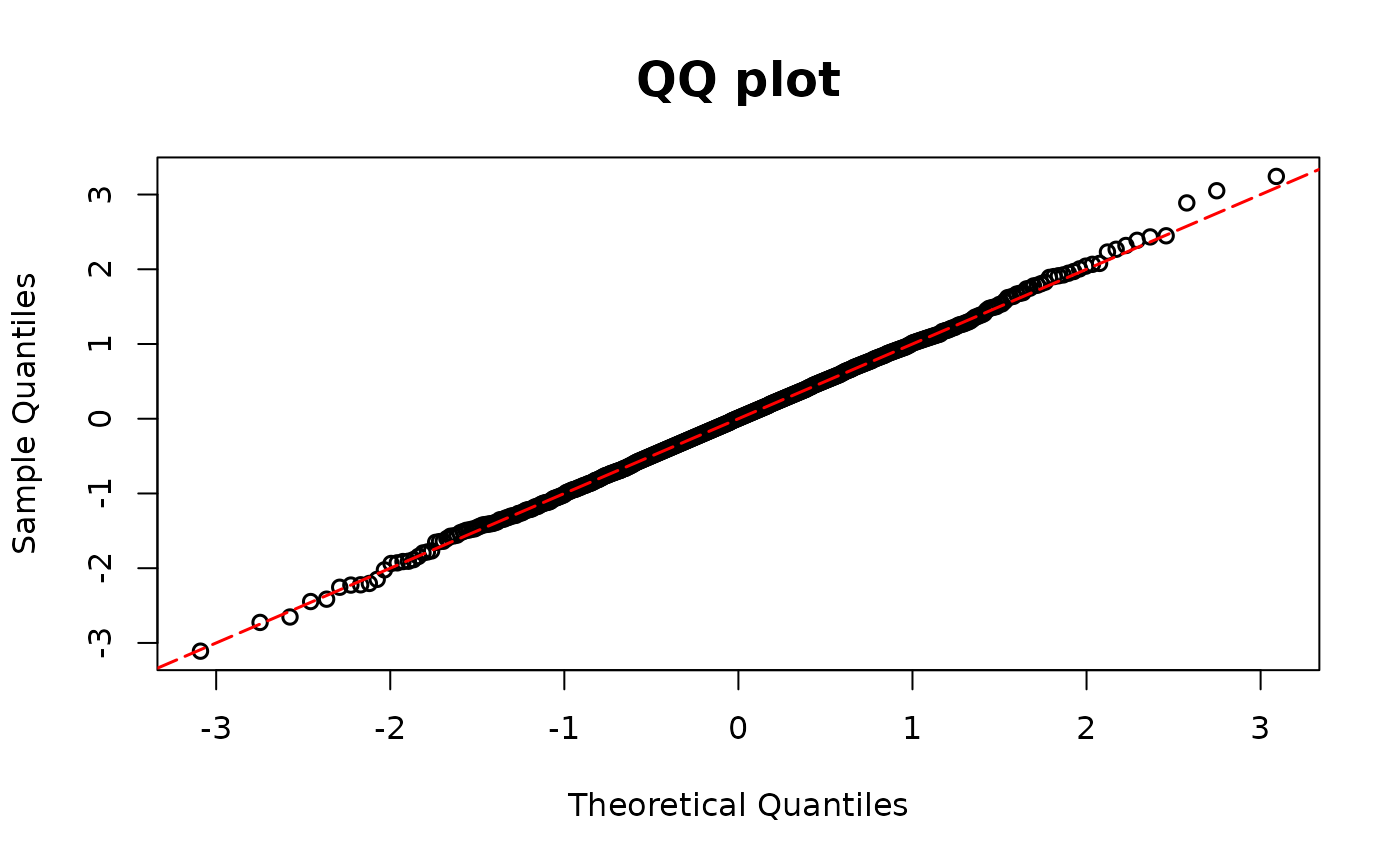
multimodel <- polr(as.factor(y1) ~ x1, method = "logistic")
resid.ord1 <- resid_disc(multimodel, plot = TRUE)
 ## Non-Proportionality
n <- 500
set.seed(1234)
x1 <- rnorm(n, mean = 2)
beta1 <- 3
beta2 <- 1
p0 <- plogis(1, location = beta1 * x1)
p1 <- plogis(4, location = beta2 * x1) - p0
p2 <- 1 - p0 - p1
genemult <- function(p) {
rmultinom(1, size = 1, prob = c(p[1], p[2], p[3]))
}
test <- apply(cbind(p0, p1, p2), 1, genemult)
y1 <- rep(0, n)
y1[which(test[1, ] == 1)] <- 0
y1[which(test[2, ] == 1)] <- 1
y1[which(test[3, ] == 1)] <- 2
multimodel <- polr(as.factor(y1) ~ x1, method = "logistic")
resid.ord2 <- resid_disc(multimodel, plot = TRUE)
## Non-Proportionality
n <- 500
set.seed(1234)
x1 <- rnorm(n, mean = 2)
beta1 <- 3
beta2 <- 1
p0 <- plogis(1, location = beta1 * x1)
p1 <- plogis(4, location = beta2 * x1) - p0
p2 <- 1 - p0 - p1
genemult <- function(p) {
rmultinom(1, size = 1, prob = c(p[1], p[2], p[3]))
}
test <- apply(cbind(p0, p1, p2), 1, genemult)
y1 <- rep(0, n)
y1[which(test[1, ] == 1)] <- 0
y1[which(test[2, ] == 1)] <- 1
y1[which(test[3, ] == 1)] <- 2
multimodel <- polr(as.factor(y1) ~ x1, method = "logistic")
resid.ord2 <- resid_disc(multimodel, plot = TRUE)