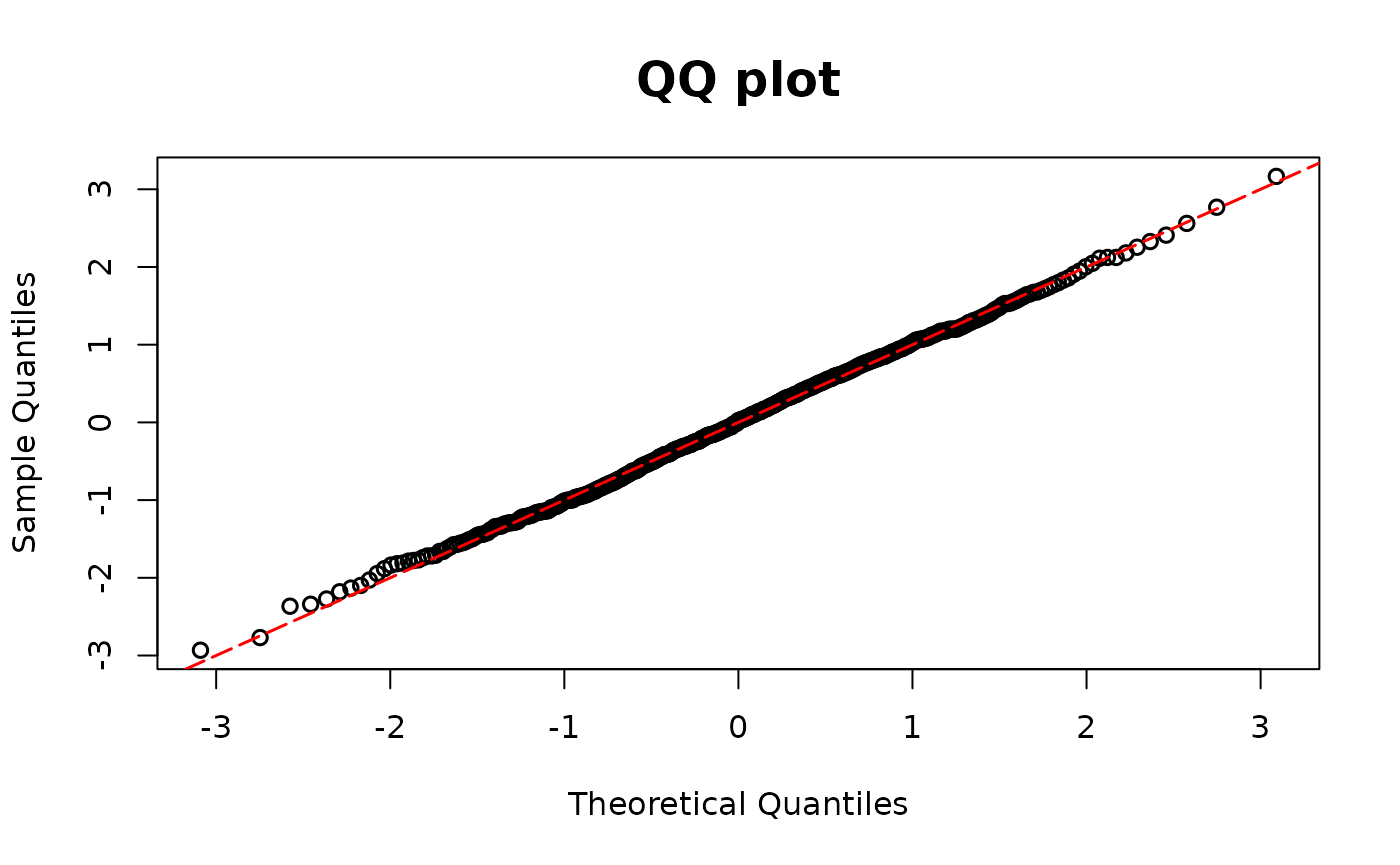
Two part models
The input arguments for the resid_2pm() function differ
from those of other functions in assessor package.
Specifically, users can utilize this function with either models or
Probability Integral Transform (PIT) as input.
For instance, in evaluating the distribution assumptions of a
two-part model that combines a logistic and a gamma regression, you
should provide the logistic regression model object as the argument for
model0 and the gamma regression model object for
model1. We recommend utilizing the model input when
assessing a gamma + logistic two-part model. Alternatively, users can
directly use the PIT as input if their two-part model is not a
gamma+logistic combination. In such cases, users should first calculate
the PIT and then input into part0 and part1,
respectively.
This function accommodates two combinations: either
model0 in conjunction with model1 or
part0 in conjunction with part1. Note that it
is essential to specify the y (outcome) values in the
function arguments.
The underlying model is a two-part model. The probability of zero is
\[p_0(\mathbf{X})=\text{logit}^{-1}\left(\beta_0+X_{1}\beta_{1}+X_{2}\beta_{2}
\right),\] where \(X_1\) is a
standard normal variable, \(X_2\) is
binary with probability of one as 0.4, and \((\beta_0,\beta_{1},\beta_{2})=(1,-2,-1)\).
A gamma distribution is employed to generate positive data. The mean
function of the positive part is described as \[\lambda_S=\exp\left(\beta_{0S}+\beta_{1S}X_1+\beta_{2S}X_2\right).\]
We let \((\beta_{0S},\beta_{1S},\beta_{2S})=(-1,-1,-2)\).
The dispersion parameter is set to be 0.5.
library(assessor)
library(MASS)
n <- 500
beta10 <- 1
beta11 <- -2
beta12 <- -1
beta13 <- -1
beta14 <- -1
beta15 <- -2
x11 <- rnorm(n)
x12 <- rbinom(n, size = 1, prob = 0.4)
p1 <- 1 / (1 + exp(-(beta10 + x11 * beta11 + x12 * beta12)))
lambda1 <- exp(beta13 + beta14 * x11 + beta15 * x12)
y2 <- rgamma(n, scale = lambda1 / 2, shape = 2)
y <- rep(0, n)
u <- runif(n, 0, 1)
ind1 <- which(u >= p1)
y[ind1] <- y2[ind1]
# models as input
mgamma <- glm(y[ind1] ~ x11[ind1] + x12[ind1], family = Gamma(link = "log")) # Gamma regression
m10 <- glm(y == 0 ~ x12 + x11, family = binomial(link = "logit")) # logistic regression
resid.models <- resid_2pm(model0 = m10, model1 = mgamma, y = y)
library(assessor)
library(MASS)
n <- 500
beta10 <- 1
beta11 <- -2
beta12 <- -1
beta13 <- -1
beta14 <- -1
beta15 <- -2
x11 <- rnorm(n)
x12 <- rbinom(n, size = 1, prob = 0.4)
p1 <- 1 / (1 + exp(-(beta10 + x11 * beta11 + x12 * beta12)))
lambda1 <- exp(beta13 + beta14 * x11 + beta15 * x12)
y2 <- rgamma(n, scale = lambda1 / 2, shape = 2)
y <- rep(0, n)
u <- runif(n, 0, 1)
ind1 <- which(u >= p1)
y[ind1] <- y2[ind1]
# PIT as input
mgamma <- glm(y[ind1] ~ x11[ind1] + x12[ind1], family = Gamma(link = "log")) # gamma regression
m10 <- glm(y == 0 ~ x12 + x11, family = binomial(link = "logit")) # logistic regression
cdfgamma <- pgamma(y[ind1],
scale = mgamma$fitted.values * gamma.dispersion(mgamma),
shape = 1 / gamma.dispersion(mgamma)
)
p1f <- m10$fitted.values
resid.pit <- resid_2pm(part0= p1f, part1 = cdfgamma, y = y)